Introducción y breve análisis
LOOP es el segundo movimiento de la Sonata para viola sola de Gyorgy Ligeti. El título se refiere a cómo las mismas figuras son repetidas con variaciones rítmicas cada vez más rápido (Ligeti, 2001). Además, Ligeti pide al intérprete tocar en el espíritu de jazz: elegante y relajado.
En este movimiento podemos encontrar influencias a Gillaume de Machaut, en cuanto al uso de la talea y el color, entendiendo el color como una serie de alturas y la talea como los ritmos que podemos ir superponiendo a ese color
La estructura de la pieza se basa en la repetición de una misma serie de 45 diadas o color (ilustración).

Consta además de una introducción formada por las cuatro primeras diadas, y una coda con esas mismas diadas, que aparecen como una novena repetición del tema que se corta abruptamente con la indicación as is torn off. Podríamos ver aquí una similitud con las obras para piano mecánico Nancarrow, donde la música finaliza súbitamente al acabar el rollo de cinta perforada.
Composición algorítmica en Loop
Para introducir este apartado, recomiendo la lectura del siguiente documento Cool Memories: Notes on the Ligeti Viola Sonata (Stulz, 2012).
Digamos que podríamos ver Loop como una matriz de o tabla de duraciones de 45x9, donde las columnas representarían cada una de las 45 diadas y las filas las 9 repeticiones. En cada casilla tendríamos un número del 1 al 8 que correspondería la duración de la diada, siendo el 1 la semicorchea.
Esta sería la matriz original de Loop:
433532233822332222463234622222233576532233822
335733222222333232532222422232322335322332222
433532233532222232322222322122321323422222121
223322222233221122231221232212321234321222222
123323221221221122232123322122132212212212122
121121122211211221321112121112213232212212121
112212212111211121221212212221111212211111211
211121112111111111211111211111111211111121111
111121112111111111111111111111111112111111111
Vemos de qué manera los números (duraciones) van disminuyendo progresivamente en cada línea y la duración total de cada una es menor, como hemos visto en el apartado anterior. Otra característica que observamos al analizar la matriz original de duraciones es que las duraciones no siempre disminuyen, aunque el resultado global de cada repeticion sea siempre menor.
En las siguiente imágenes podemos observar la evolución de las duraciones en la primera y segunda diadas: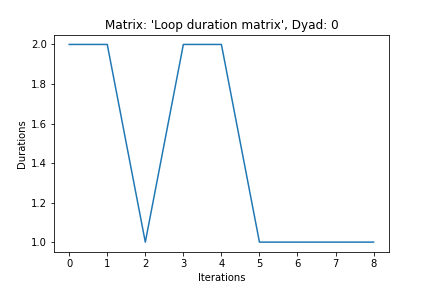
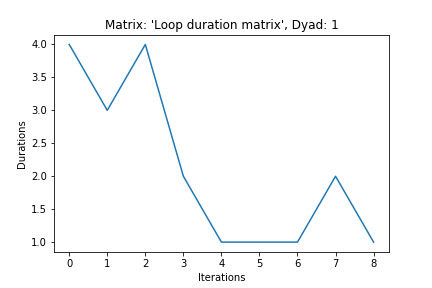
Una posible explicación de este proceso podría ser la aplicación de una función de probabilidad de disminución a cada una de las filas.
Siendo I1 la primera línea, tendríamos:
I1
I2=f(I1)
I3=f(I2)
I4=f(I3)
……
Una de las propuestas de Stulz es la generación de cada fila por una distribución de probabilidad, esto es contar cuantas veces aparece cada número en una determinada fila.
Por ejemplo, en I2 tendríamos las siguientes distribuciones de probabilidad:
|
Duraciones |
2 |
3 |
4 |
5 |
8 |
|
Probabilidad de aparición en I2 |
24/45 |
16/45 |
1/45 |
3/45 |
1/45 |
Este análisis sería necesario realizarlo para cada una de las 8 repeticiones.
Otra posible forma de generación de esta matriz de duraciones sería mediante cadenas de Markov. En una cadena de Markov la probabilidad de un evento depende del evento anterior, es decir, tiene memoria. En nuestro caso podríamos decir que Loop, en lugar de ser azaroso es generativo. Veríamos cada una de las 45 diadas como átomos que evolucionan en el tiempo, y su valor en la siguiente repetición dependerá del valor que tenga en el momento actual.
La mejor manera de representar este proceso es mediante una tabla de transición, donde en la columna izquierda tenemos las posiciones actuales y en las siguientes podemos visualizar la probabilidad de ocurrencia futura. Así, una duración de 2 tendrá en I2 una probabilidad de 13/19 de continuar siendo 2 y una probabilidad de 6/19 de valer 3. Sin embargo, una posición actual de 3 tendría una probabilidad de 8/14 de valer 2, 5/14 de valer 3 y 1/14 de valer 5.
De la misma manera tendríamos que realizar este análisis para cada una de las repeticiones.
Una última opción que podríamos tener en cuenta sería la de obtener una matriz global de Markov, en lugar de una para cada repetición, que nos permitiera obtener las duraciones para cualquiera de las iteraciones.
Explicación de la aplicación
En la aplicación que hemos creado intentamos facilitar todos estos procesos.
En primer lugar podremos escoger la generación de las duraciones de la primera presentación del color.
Escogeremos entre las duraciones originales de Loop o una distribución de probabilidad del mismo original.
Decidiremos después la forma de generación del resto de la matriz:
Las duraciones originales de Loop
Generación mediante una matriz global de Markov
Generación por distribución de probabilidad
Generación mediante una cadena de Markov para cada repetición.
Al pulsar el botón GENERAR obtendremos por un lado una matriz de duraciones, además de una gráfica de dicha matriz.
Obtendremos además la partitura, con la introducción y coda propuesta por Ligeti. Podremos descargarla en formato PDF, XML y MIDI. Este último nos permitirá escuchar fácilmente el resultado.
En la partitura hemos añadido algunas anotaciones de matices que se repiten en la partitura original. Pero no debemos olvidar que Ligeti, aun inspirándose en la Matemática, toma muchas de sus decisiones de manera experimental. En este caso estas se corresponderían con los matices, arcos articulaciones, acentos, etc.
Referencias:
Ligeti, G. (2001). Sonata for Viola Solo. Mainz: SHOTT.
Stulz, J. (2012). Cool Memories: Notes on the Ligeti Viola Sonata. Recuperado de http://www.johnstulz.com/photos/ligetinotes.pdf
Ir a la aplicación de "loop"
Volver a la página principal